Object Oriented Scheduling - Part I
I mentioned in a previous post that traditional CPM scheduling is rather primitive. It has only two major objects, tasks and dependencies. You might suggest that resources are also worthy of considering, but actually in software like Microsoft Project it can be argued that they are a bit of an afterthought. My contention is that tasks and even the schedule itself is but one facet of a project, but before we get to building a better model for that let's look at how the current model can be improved. One way to do this is to improve the behavior of the tasks themselves. We can do this by adding additional properties or parameters which will change the way the tasks behave under different conditions.
The first and one of the more obvious properties of a task is the elasticity. We know that some tasks are quite fixed in duration while others are more flexible. Indeed, it is common to desire a task which will stretch automatically for the length of a project or a certain phase of a project. This sort of task is often called a "hammock task" and the method for creating one in Project is rather convoluted. Between the two extremes there are a range of flexibility in the durations of tasks. This may be due to the availability of resources upon demand (brought in to keep a task on schedule if necessary) or perhaps a lower priority or maybe the task results in something "nice to have" rather than something required.
Current scheduling software can not distinguish between the black of the fixed duration and the white of the hammock task, and as a result minor shifts in a flexible task impact the schedule projection to the same extent as a task with a hard duration. We can work around this by adding lag to the dependencies or other tricks, but ultimately we have to exercise judgement in determining if any slip is "real".
To get around this and to maintain a more stable model, consider adding a property to a task which determines its flexibility. Here I model the property as a spring.
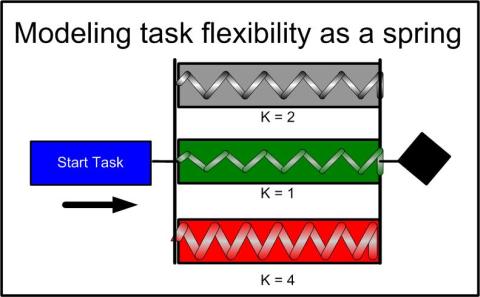
Springs have a constant "k" which describes their flexibility. We could simply add a k property to tasks. A higher k would indicate a very stiff task and a low or 0 k would indicate that a task was quite flexible. Using the values of k and a measure of how much schedule pressure there is, we could obtain a more realistic model of how the work will actually be performed. Calculation of a network made of springs is more complex than the traditional critical path, but it should be nearly trivial for a modern computer. Why don't we start doing this now?
There are several more properties and methods I'll be describing in the coming days. Your comments are always welcome.
