Glen asked what the "underlying principle" for the 80/20 rule is. So instead of letting things get lost in the comments I'm going to give a brief summary of what I know about it.
Vilfredo Pareto was a French-born Economist who on studying land distribution in Italy found that 80% of the land was owned by 20% of the population. Essentailly he found that land distribution followed a power law probability distribution and conveniently 80/20 happens to be one of the most easily spotted points on the curve. You can see that when I graph it in excel a big red arrow shows up and points at it! I'm not familiar with all of the mathematics behind it, but it does serve as a useful rule of thumb and has been adopted by many people as a "rule".
With the easy availability of large data sets (website log data) and the use of excel, it seems to show up quite frequently. In an internal blogging system where I work the ratio of posts seemed to follow this "rule"
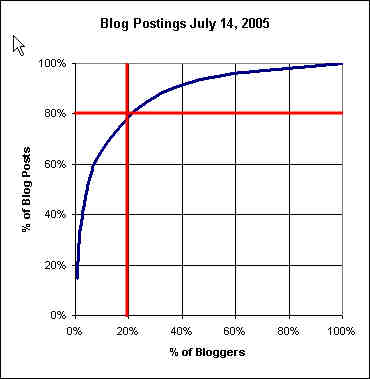
Well, it seemed to follow that rule until I realized that I counted all people with a blog and 1 or more posts. If I added in the bloggers who had never posted it threw the curve off. Anyway, fundamentally I think it is more of an observation than a rule. Juran, who you might know from his work in quality management took the ball and ran with it creating the Pareto Principle and derivatives thereof.
That it fits certain observed phenomena is interesting in the same way that PI or PHI (1.61803398874989... also known as the Golden Section) is interesting. As Glen has pointed out to me it is also related to Theodore Sturgeon's maxim that "80% of everything is crap". This and a bit of recursion will get us most of the way to 100%. I'll leave a little room here at the bottom to keep the ratio golden.

Comments (3)
Jack,
I poked around a bit but no indication as to "why" the 80/20 rule exists. Other "rules" are derived from things like Poisson arrival times, simplifications of underlying probability distributions (the PERT formula for example is a simplification of the Triangle or Beta distribution).
One of the first observations of the Poisson process was that it properly represented the number of French cavalry soldiers
that died as a result of being kicked by a horse. "Rescherches sur la Probabilite des Jugements en Matiere Criminelle et en Matiere Civile, Precedees des Regles Generales du Calcul des Probabilities," Simeon D. Poisson, 1837.
Phi's source can be found in the nice little Dover paperback "The Golden Ratio." Pi of course comes from the ratios obsevred by Greeks sitting under trees with nothing else to do except contemplate their navel.
Posted by Glen B. Alleman | October 21, 2005 9:08 AM
Posted on October 21, 2005 09:08
From what I understand, many power law distributions are determined from observation:
http://aps.arxiv.org/PS_cache/cond-mat/pdf/0412/0412004.pdf
And thus may have various causes. I also think (as I sort of stated) that the knee of any sort of power law curve is visually around the same place and that place is near 80/20. Given a continuous smooth curve I'd expect that dividing it in 5ths is a reasonable way to look at it. If we do that then only certain points are worth looking at. 100 is boring. 0 is boring, 50/50 is not on a most non-linear curves. 80/20 seems to fit on the curve so we pick it and our perception seems to pivot around that point. It is easy to find what we are looking for and to adjust data to achieve it. I left unstated that I removed the hits to the website that I generated by posting and editing the site. That would have shifted the curve to something like 80/17. I mentioned this explicitly in my second blog post.
I'd suggest that many curves like this fit phenomena which are self-referential or recursive in a way. Reading blogs does have a component of this as often a single reader refers others - this multiplies the power of the frequent readers. In addition, people who happen upon the blog and don't care for it don't come back and don't make any further references.
Anyway, I'm not sure I have enough energy or mathematical skills to get to the bottom of it, but if you find anything out, let me know.
Posted by jack | October 21, 2005 9:47 AM
Posted on October 21, 2005 09:47
i want some body provhde me some articles about 20-80 rule in education how can we apply on kidds and cheldern
thanks
counselor
Posted by moe | July 10, 2007 8:45 AM
Posted on July 10, 2007 08:45